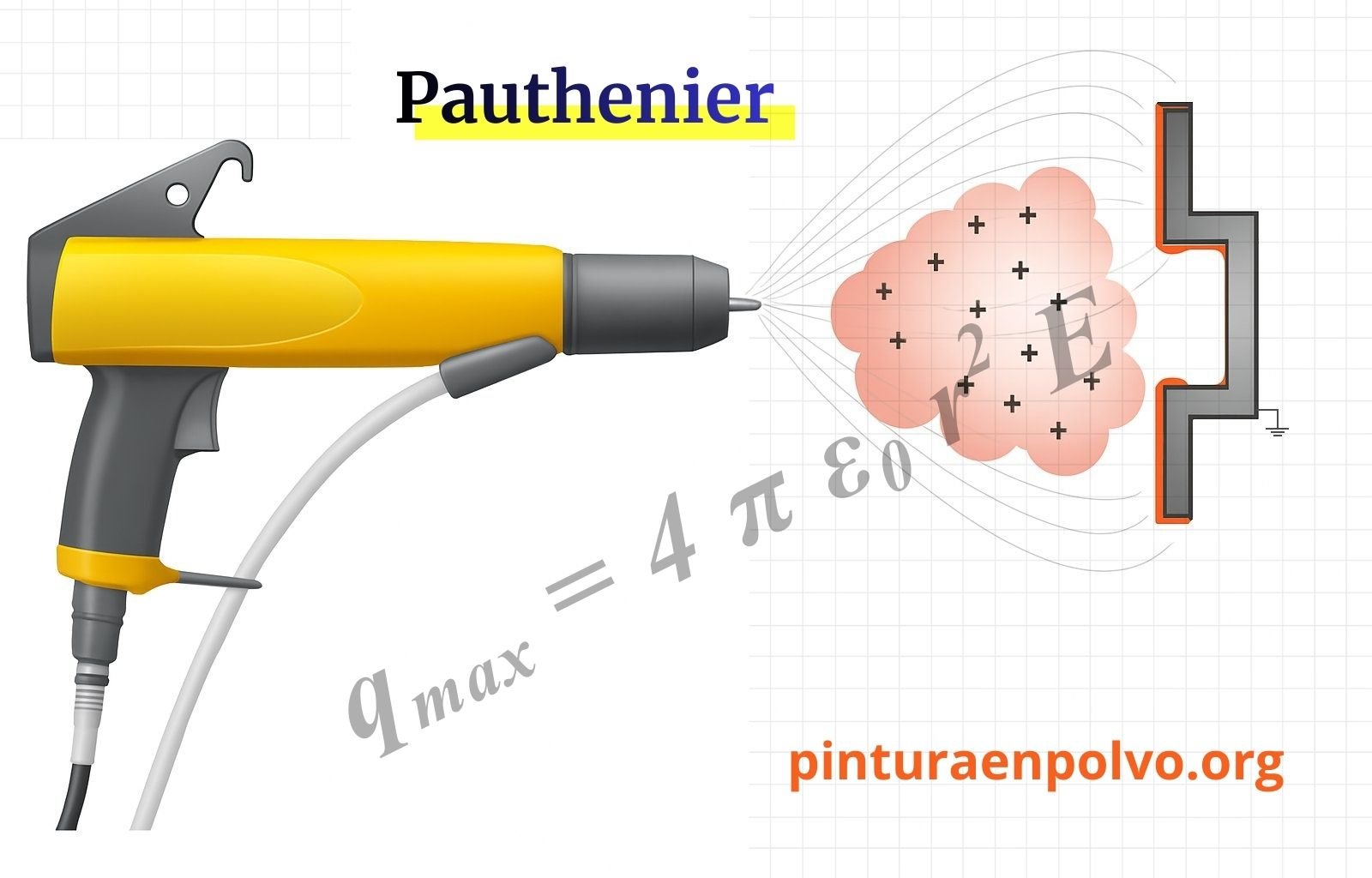
En los procesos de pintura electrostática en polvo, la eficiencia de aplicación y la calidad del recubrimiento están directamente condicionadas por la cantidad de carga eléctrica que pueden adquirir las partículas de polvo.
La ecuación de Pauthenier proporciona un marco teórico fundamental para comprender el límite físico de carga de una partícula y, por tanto, para interpretar fenómenos habituales en planta que no pueden explicarse únicamente aumentando el voltaje o la corriente. Por ejemplo, determinados defectos que aparecen de forma sistemática a partir de ciertos umbrales operativos.
El concepto clave: la saturación de carga
Durante la carga corona, las partículas de polvo se cargan por impacto con iones generados en el electrodo. Sin embargo, esta carga no aumenta indefinidamente. Existe un punto en el que el campo eléctrico generado por la propia partícula compensa el campo externo, impidiendo que sigan depositándose más cargas sobre su superficie.
Este fenómeno se conoce como saturación de carga y a partir de ese punto, el sistema entra en un régimen dominado por repulsión electrostática, no por atracción hacia la pieza.
La ecuación de Pauthenier describe precisamente ese límite de carga.
Para una partícula esférica aislada sometida a un campo eléctrico uniforme la carga máxima que admite viene dada por la siguiente ecuación (simplificada):
![]()
Donde:
- qmax es la carga máxima que puede adquirir la partícula
- ε0 es la permitividad del vacío
- r es el radio de la partícula
- E es la intensidad del campo eléctrico
Este valor representa un límite teórico superior de carga, independiente del tiempo de exposición o del incremento adicional de kV pero dependiente de la geometría de la partícula y de la intensidad del campo eléctrico.
Para analizar los fenómenos que ocurren en la aplicación de pintura en polvo conviene expresar la ecuación como “carga por unidad de masa”, q/m
![]()
Donde ρ es la densidad del polvo (vale lo mismo el peso específico)
Una implicación práctica directa:
Cuanto menor es el tamaño de partícula, mayor es la carga específica y por tanto es mayor la repulsión polvo-polvo.
La conclusión práctica es evidente: “Una pintura con un exceso de fracción fina produce una pérdida de penetración en cavidades y plegados”
Esto conecta directamente la ecuación de Pauthenier con la gestión granulométrica, la estabilidad de la nube de polvo y la eficiencia de transferencia.
Veamos ahora la interacción con los parámetros del proceso
Incremento del Voltaje aplicado (kV)
El aumento de kV incrementa el campo eléctrico solo hasta que la mayoría de las partículas alcanzan saturación. Más allá de ese punto:
- no aumenta la masa depositada
- se intensifica la repulsión electrostática
- se degrada la uniformidad del film
Desde un punto de vista de proceso, el kV óptimo es aquel que sitúa al sistema ligeramente por debajo del régimen de saturación generalizada.
Este fenómeno desmonta la idea operativa de que «más kV siempre es mejor».
Incremento de la Corriente aplicada (µA)
El aumento de corriente incrementa la densidad de iones disponibles, pero no modifica el límite de carga de Pauthenier. Por tanto:
- subir µA no evita la saturación
- pero sí puede acelerar defectos asociados a sobrecarga superficial y back-ionization
Espesor de película
A medida que el espesor de pintura aumenta, el campo eléctrico efectivo sobre la superficie disminuye. Esto, combinado con la saturación descrita por Pauthenier, explica:
- la dificultad para seguir cargando capas gruesas
- la aparición de límites naturales de espesor en una sola pasada
Relación con fenómenos críticos de planta
La ecuación de Pauthenier ayuda a interpretar correctamente algunos fenómenos habituales en cabina como son:
- Efecto jaula de Faraday: zonas donde el campo eléctrico se anula localmente
- Back-ionization: acumulación excesiva de carga en superficies aislantes
- Baja eficiencia de transferencia a altos kV
- Repulsión polvo–polvo en atmósferas muy cargadas
Desde esta perspectiva, estos fenómenos no son fallos del equipo, sino consecuencias directas de los límites físicos de la carga electrostática.
Limitaciones del modelo teórico
Es importante recalcar que la ecuación de Pauthenier realiza algunas suposiciones:
- Asume partículas esféricas aisladas
- Considera un campo eléctrico uniforme
- No incluye efectos de resistividad, humedad, turbulencia ni interacción entre partículas
Por tanto, debe utilizarse como herramienta de diagnóstico conceptual, y como soporte técnico para justificar ajustes en la producción.
Veamos un ejemplo
Caso real de cabina: sobrecarga por aumento de kV
Situación inicial:
Cabina automática con pistolas corona aplicando polvo epoxi–poliéster.
- Granulometría de la pintura: d50 ≈ 32 µm, fracción fina significativa (<15 µm)
- Parámetros iniciales:
- Voltaje: 70 kV
- Corriente: 20 µA
- Distancia pistola–pieza: 25 cm
Resultados:
- Buena cobertura general
- Penetración aceptable en geometrías medias
- Espesor medio: 70–80 µm
Acción correctiva mal planteada
Ante una falta de cobertura puntual en zonas interiores, se decide:
- aumentar el voltaje a 90 kV
- mantener corriente y resto de parámetros
Hipótesis operativa: mayor campo eléctrico significa mayor deposición
Resultado observado en planta
Tras el ajuste se observa:
- que empeora la penetración en cavidades
- hay un aumento del rebote de polvo (back-ionization)
- superficie exterior con sobrecarga aparente en áreas cercanas a cavidades
- caída de la eficiencia de transferencia
- necesidad de mayor consumo para alcanzar espesor objetivo
Interpretación mediante la ecuación de Pauthenier
Con el incremento de kV:
- el campo eléctrico local aumenta
- las partículas finas alcanzan rápidamente su carga de saturación
- como hay una fracción significativa de partículas finas el sistema entra en régimen dominado por repulsión electrostática
Según Pauthenier la carga máxima por partícula está limitada por r2 E y una vez alcanzado ese límite, más campo no implica más polvo depositado
En cavidades ocurre que el campo eléctrico efectivo ya es bajo por geometría y la saturación global de la nube agrava el efecto jaula de Faraday
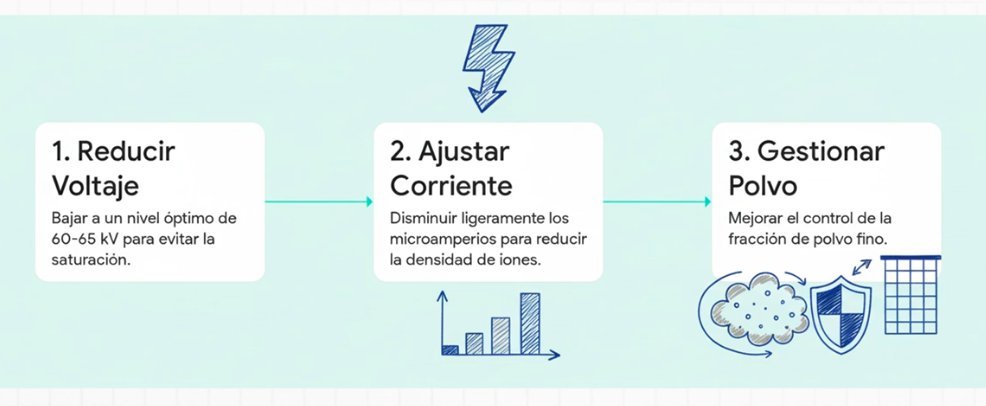
Corrección basada en este criterio
Se aplican los siguientes ajustes:
- reducción del voltaje a 60–65 kV
- ligera disminución de µA
- aumento controlado del tiempo de aplicación
- mejora de la gestión de fracción fina (cribado / reposición)
Resultados:
- reducción de repulsión polvo–polvo
- mejora evidente de la penetración
- aumento de eficiencia de transferencia
- mayor regularidad del espesor en las distintas zonas de la pieza
Lección de proceso
Este caso demuestra que la optimización pasa por trabajar por debajo del régimen de saturación. Tener en cuenta que el “límite de Pauthenier” se alcanza antes de lo que indica la intuición operativa y que finalmente aumentar kV puede empeorar el resultado global
Para ingeniería de proceso, la ecuación de Pauthenier permite anticipar este comportamiento y evitar ajustes empíricos contraproducentes.
Conclusión técnica
La ecuación de Paulthenier permite pasar de un enfoque empírico a uno físicamente fundamentado en la aplicación de pintura en polvo. Su correcta comprensión ayuda a:
- definir límites realistas de proceso
- reducir ensayos innecesarios
- mejorar repetibilidad y estabilidad
- formar equipos técnicos con criterio ingenieril
Para un responsable de línea de aplicación o simplemente para el operador eficiente, conocer la ecuación de Pauthenier permite entender los límites reales del proceso, evitando ajustes que no aportan mejora y solo generan problemas.
El razonamiento basado en la explicación de Pauthenier abre la puerta a hilar más fino en situaciones complicadas en la aplicación de la pintura en polvo.
Situaciones que veremos en próximos artículos.